진법 변환

주어진 수를 다른 진법으로 변환하는 것을 ‘진법 변환’이라고 합니다. 일상생활에서 10진법을 주로 사용하지만, 12진법과 60진법도 함께 사용합니다. 연필 1 다스를 12자루, 1 그로스(Gross)를 12 다스, 1피트(Feet)를 12인치(Inch)로 바꾸는 등 단위를 나타낼 때는 12진법을 사용하고, 1시간을 60분, 1분을 60초, 원의 각도를 360도 등과 같이 시간이나 각을 나타낼 때는 60진법을 사용합니다.
2진수, 8진수, 12진수 -> 10진수
2진수, 8진수, 16진수를 10진수로 변환하는 방법을 알아봅시다.
2진수, 8진수, 16진수 0> 10진수
각 자리의 숫자에 자릿값을 곱한 후 모두 더합니다.
예) 2진수 1011은 각 자리의 자릿값 2
3
, 2
2
, 2
1
, 2
0
을 해당 자리의 숫자와 곱한 후 모두 더하여 구합니다.
1011
(2)
= 1 X 2
3
+ 0 X 2
2
+ 1 X 2
1
+ 1 X 2
0
= 11
(10)
2진수 0.1, 8진수 135, 16진수 20C를 10진수로 변환하는 과정은 다음과 같습니다.
0.1
(2)
= 1 X 2
-1
= 1 X 1/2 = 0.5
(10)
135
(8)
= 1 X 8
2
+ 3 X 8
1
+ 5 X 8
0
= 64 + 24 + 5 = 93
(10)
20C
(16)
= 2 X 16
2
+ 0 X 16
1
+ 12(C) X 16
0
= 512 + 0 + 12 = 524
(10)
10진수 -> 2진수, 8진수, 16진수
10진수를 다른 진수로 변환할 때 유의할 점은 소수점이 있는 경우 정수 부분과 소수 부분의 변환 과정이 다르다는 점입니다. 소수점이 있으면 정수와 소수 부분을 구분하여 변환하고 결과를 다시 조합해야 합니다. 10진수를 다른 진수로 변환하는 방법은 모두 같으므로 기본적으로 2진수를 알아봅시다.
정수 부분의 변환
10 진수의 정수 부분을 2진수로 변환하는 방법입니다.
10진수 정수 부분 -> 2진수
1. 10진수의 정수 부분을 2진수의 밑수 2로 나누어 몫과 나머지를 구합니다.
2. 몫이 더 이상 나누어지지 않을 때까지 밑수 2로 계속 나눕니다.
3. 각 단계의 나머지를 나눈 역순으로 나열합니다.
예) 10진수 19는 몫이 더 이상 나누어지지 않을 때까지 계속 2로 나눈 후, 몫이 2보다 작아질 때 각 단계의 나머지를 역순으로 나열하면 2진수 10011이 됩니다.
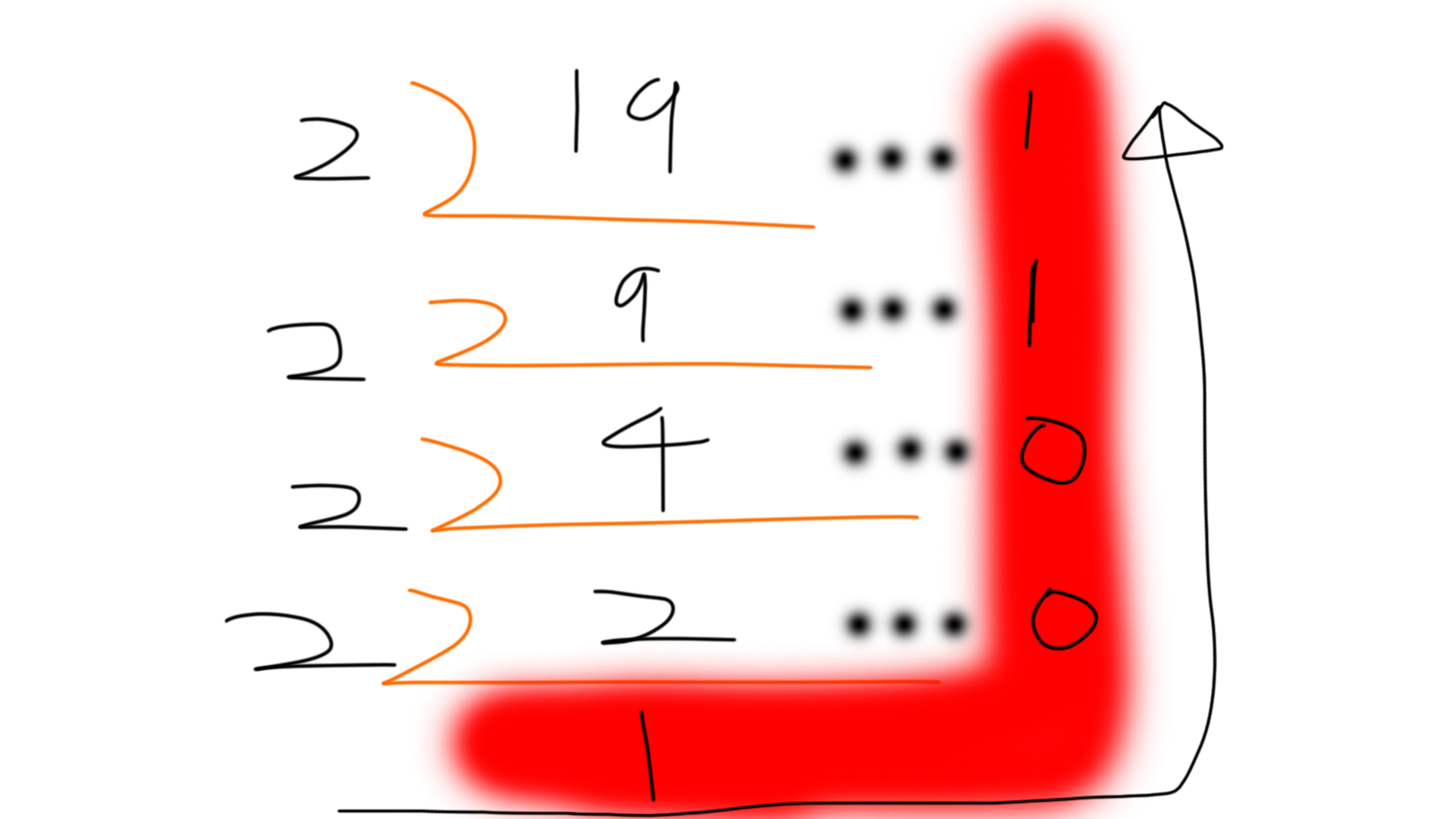
19
10
= 10011
(2)
다른 예를 들어보도록 하겠습니다. 10진수 52를 16진수로 변환하는 과정은 아래 그림과 같습니다. 52를 16으로 나눈 후 나머지를 역순으로 나열하면 16진수 34가 됩니다.
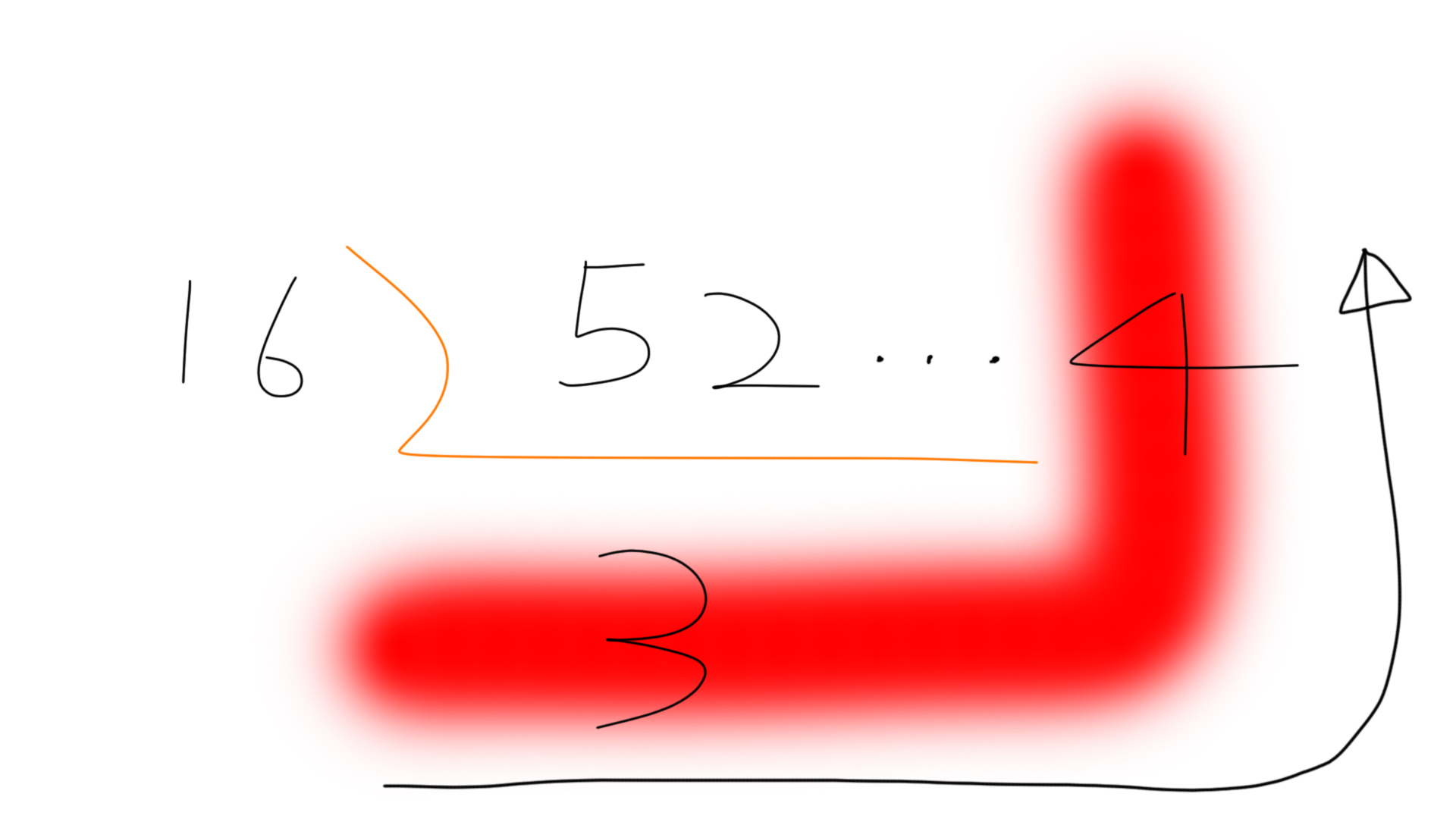
52
(10)
= 34
(16)
소수 부분의 변환
10진수의 소수 부분을 2진수로 변환하는 방법을 알아봅시다.
10진수 소수 부분 -> 2진수
1. 10진수의 소수 부분에 2진수의 밑수 2를 곱한다.
2. 곱셈 결과로 소수 부분이 0이 될 때까지 밑수 2를 계속 곱한다.
3. 각 단계에서 발생하는 정수 부분(자리올림)을 순서대로 나열한다.
예) 10진수 0.125는 소수 부분이 0이 될 때까지 2를 계속 곱한다. 그리고 각 단계에서 발생하는 정수 부분(자리올림)을 순서대로 나열하면 2진수 0.001이 된다.
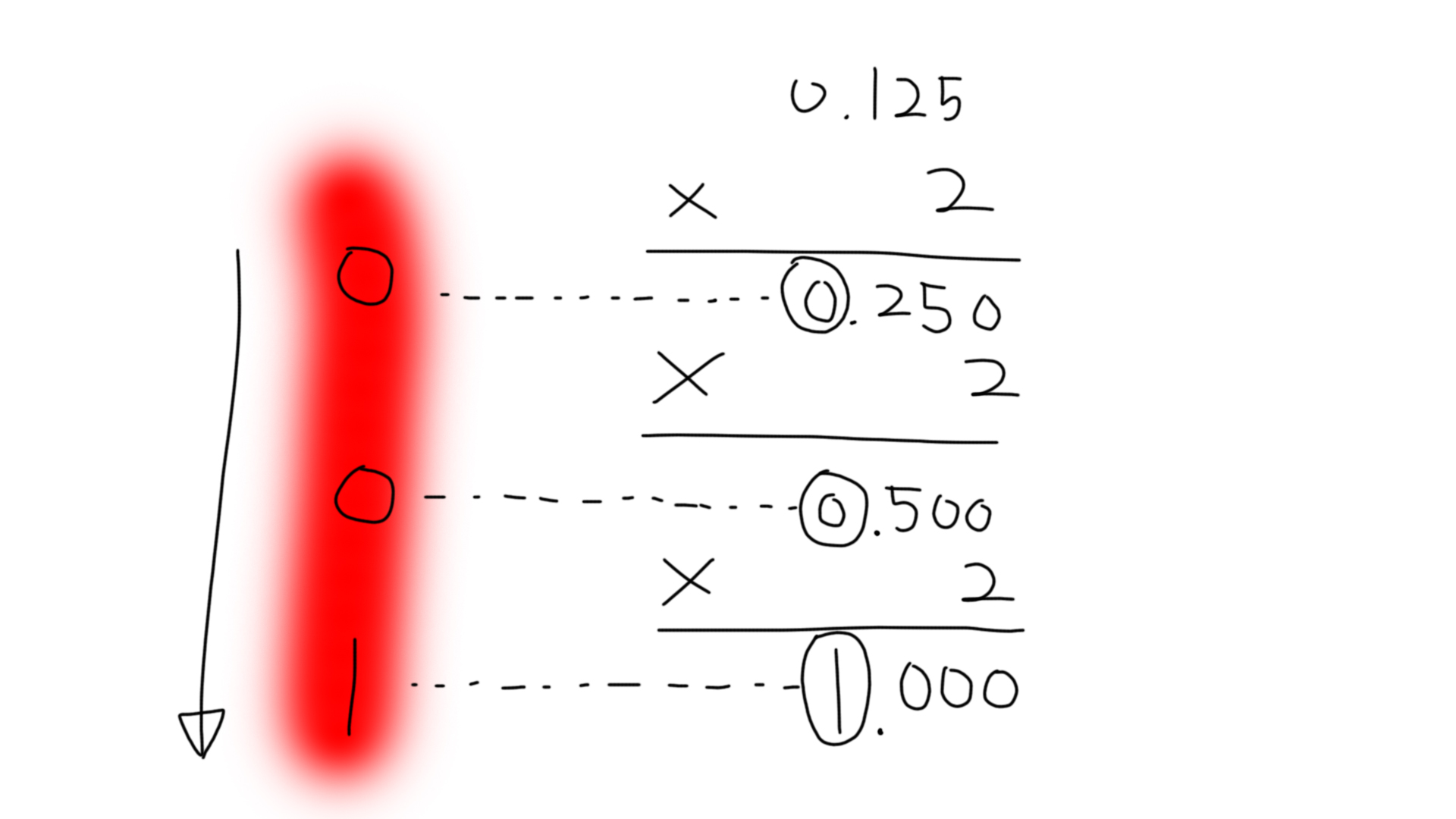
0.125
(10)
= 0.001
(2)
다른 예로 10진수 52.375를 8진수로 변환하는 과정을 살펴봅시다. 먼저 정수 부분 52를 8로 나누어 나머지를 역순으로 나열하면 8진수 64가 됩니다. 그리고 소수 부분 0.375에 8을 곱한 결과로 발생하는 정수 부분을 나열하면 8진수 0.3이 됩니다. 따라서 정수 부분과 소수 부분의 변환 결과를 조합하면 10진수 52.375는 8진수 64.3이 됩니다.
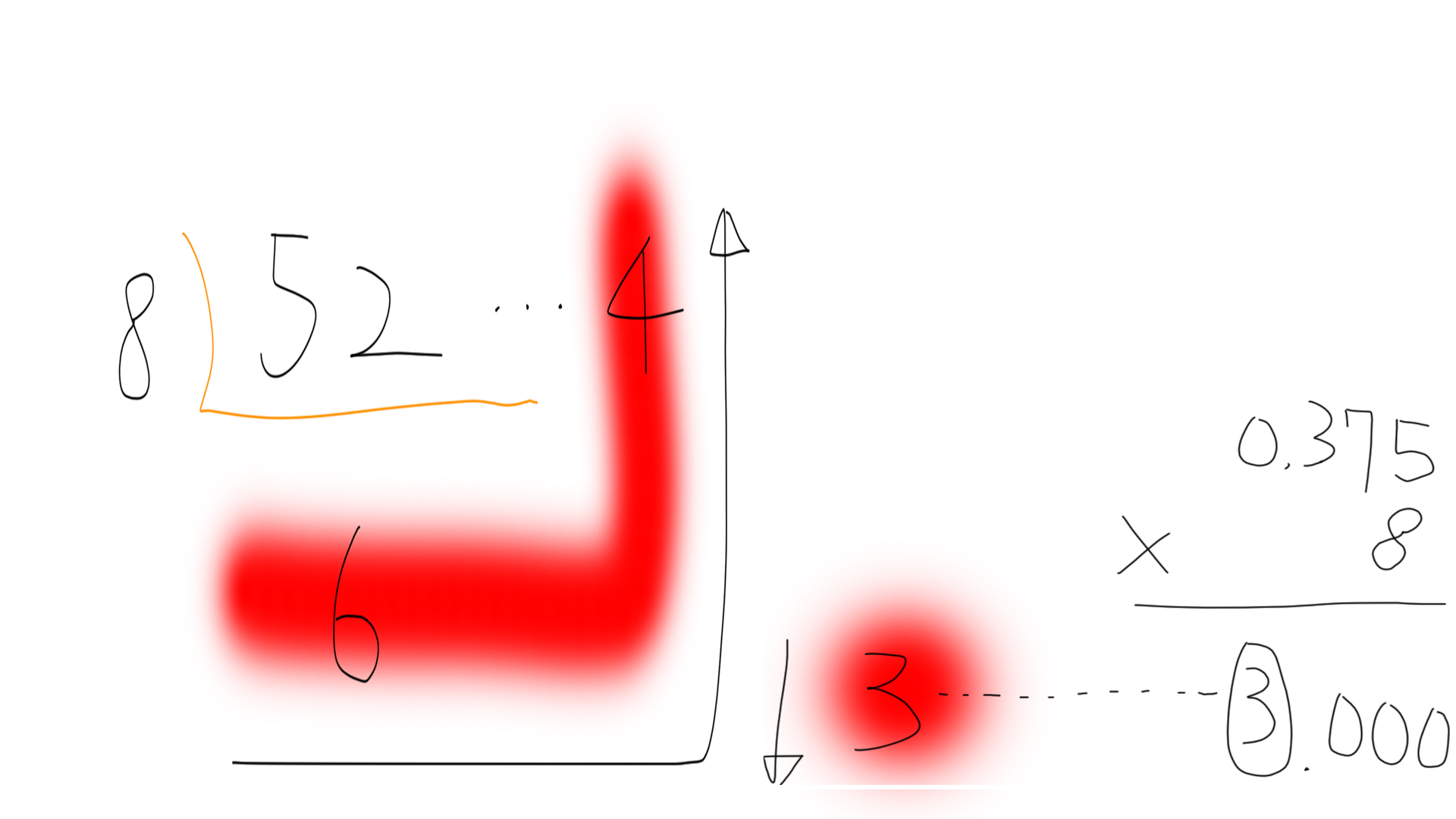
52.375
(10)
= 64.3
(8)