수의 체계

기원전 2000년경 고대 수메르에서는 60을 밑수로 하는 60진법을 사용했습니다. 로마 시대에는 12를 밑수로 하는 12진법을 사용했으며 현재 우리는 0~9의 숫자 10개를 사용하는 10진법을 사용합니다.
컴퓨터에서도 이러한 진수들을 사용하며 사용하는 수 체계에 대해 공부해보도록 하겠습니다.
진법
은 임의의 수를 숫자로 표현하는 방법입니다. 임의의 수를 10진법으로 표현하면 10진수가 되고, 2진법으로 표현하면 2진수가 됩니다.
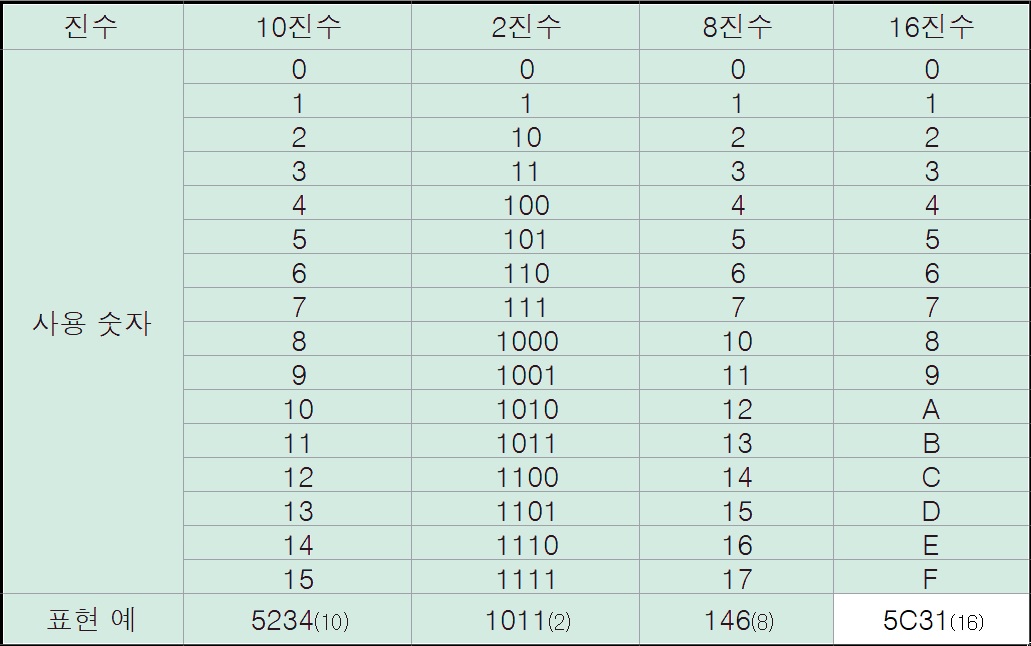
현재 우리가 사용하는 디지털 컴퓨터는 두 개의 전기 신호(0 또는 1)를 이용해 정보를 표현합니다마는 십만, 백만과 같이 큰 수의 경우 2진수로 나타내면 자릿수가 너무 길어 읽기가 불편하기 때문에, 2진수와 상호 변환이 쉽고 자릿수도 짧은 8진수와 16진수를 함께 사용합니다. 진수의 수 표기와 같이 8진법은 숫자 8개(0~7), 16진법은 숫자와 문자 16개(숫자 0~9, 문자 A~F)를 사용합니다. 일반적으로 수의 오른쪽에 아래 첨자의 형태로 진법을 나타내는 숫자가 붙습니다.


예를 들어 10진수 5234의 자릿값을 알아보면 5는 10 ³(1000), 2는 10²(100), 3은 10 ¹(10), 4는 10⁰(1)이 됩니다.
10진수 5234를 구하려면 각 자리의 숫자와 자릿값을 곱한 후 더하면 됩니다.
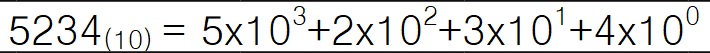
2진수 101.1, 8진수 146, 16진수 5C3의 자릿값은 다음과 같습니다.
101.1
(2)
: 1의 자릿값 = 2
2
, 0의 자릿값 = 2
1
, 1의 자릿값 = 2
0
, 1의 자릿값 = 2
-1
146
(8)
: 1의 자릿값 = 8
2
, 4의 자릿값 = 8
1
, 6의 자릿값 = 8
0
5C3
(16)
: 5의 자릿값 = 16
2
, C의 자릿값 = 16
1
, 3의 자릿값 = 16
0